Analisi di funzioni non approssimabili pt.1

Buondì!

Oggi andremo a toccare un'altra corda della matematica, ed è quella dell'analisi

Ma non l'analisi tradizionale...

Sarebbe troppo facile

Ma un analisi su funzioni casuali iterative

Ovvero non sempre rappresentabili perfettamente da una funzione matematica

Scotta eh, pronti?

- - - - - - - - -

Ok, prendiamo un grafico a caso, calcolato casualmente tra -2 e 2

Bene, sembra abbastanza casuale

O almeno abbastanza per non poterlo approssimare facilmente...

Ora, per capire meglio il grafico funzione, potremmo calcolarne la prima derivata, poi seconda, poi terza, fino a che necessario allo studio

Ma la domanda è: come si calcola la derivata di una funzione non matematicamente approssimabile?

A questo punto ero sul punto di lasciar perdere, quando ho pensato al concetto di derivata: la velocità di cambiamento di una curva

Dunque, essendo ( v = s / t ) e prendendo intervalli di tempo di 0.01s (piccoli)

La derivata ad un punto x[n] sarebbe ( x[n+1] -  x[n] ) / 0.01 = 100 * ( x[n+1] -  x[n] )

Che è proporzionale allo spazio ( x[n+1] -  x[n] )

Dunque, la "derivata prima" del grafico sarebbe così:

Ok, interessante...

Non quello che mi aspettavo, devo dirlo...

Qua il problema è che stiamo considerando tanto "rumore" nella funzione, e ciò porta a queste grandi oscillazioni

Ok, allora possiamo arrotondare queste asperità?

Potremmo, ma come vediamo, le "asperità" compongono la maggior parte del grafico, e non avrebbe molto senso...

Altre idee?

Potremmo calcolare derivate superiori!

Come la seconda derivata:

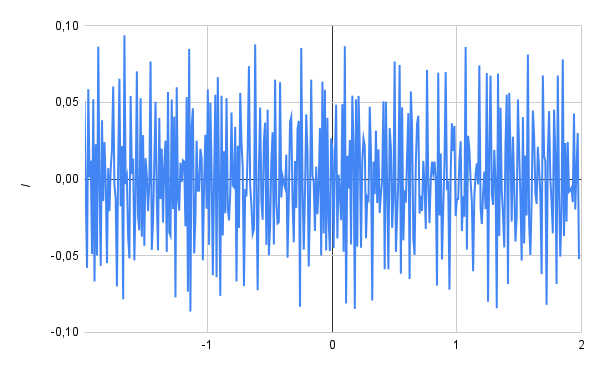
Notiamo subito che il range y qua è aumentato

E se provassimo a calcolare derivate superiori andremmo a trovare dei grafici con insieme immagine sempre più larga (l'estensione del grafico per l'asse y)

Quindi, derivate superiori non ci dicono niente...

Ok, allora potremmo calcolare una regressione del grafico della prima derivata?

Certamente!

Se ci proviamo (regressione lineare), verrebbe fuori una retta con coefficente angolare vicino allo 0, ma comunque positivo

Ciò cosa significa?

Significa che la velocità di cambiamento aumenta nel tempo!

E una regressione sulla seconda derivata?

Sarebbe una retta con coefficente angolare ancora più piccolo, a questo punto trascurabile

Quindi, essendo la seconda derivata l'accelerazione, scopriamo che essa è costante ( f''(x) = k )

Dunque, ragionando:

f''(x) = k

f'(x) = kx

f(x) = k/2! • x²

Scopriamo che una buona approssimazione per il grafico di partenza è una funzione quadratica ( almeno per il range -2 / 2 )

Quindi? Ora?

Giusta osservazione

Sapere che la funzione è approssimabile ad una quadratica non porta a niente di per se...

(Tra l'altro, se avessimo definito i coefficienti angolari delle regressioni delle derivate successive mai realmente trascurabili, potremmo raggiungere polinomi di grado infinitesimo)

Quindi? Come si fa?

Abbiamo introdotto alcuni concetti che potrebbero tornare utili, ma per ora ci fermiamo qui!

- - - - - - - - -

Ok, oggi è stata un po' blanda...

Ma abbiamo introdotto un nuovo argomento!

Quindi come sempre, vi auguro un buon proseguimento di giornata e...

Al prossimo post