Derivate e come vengono usate nella vita comune | pt. 1

Rieccomi...

In questi giorni ho avuto diversi impegni che mi hanno tenuto lontano da casa per molto tempo

E dunque non sono riuscito a trovare tanto tempo per pubblicare...

Tuttavia, problema = opportunità, dunque ho avuto qualche giorno in più per esplorare questo argomento: Le derivate

Un concetto difficile per chi lo approccia, che diventa banale per chi lo perfeziona

- - - - - - - - -

Ma prima di tutto, cos'è una derivata?

Una derivata è una funzione denominata generalmente con f'(x), che ha come scopo quello di mostrare l'andamento del tasso di crescita istantaneo di una funzione f(x)

Eh?

Ok, la rendo più comprensibile

Prendiamo una funzione f(x) = x²

E la sua derivata f’(x) = 2x      (Spiegherò come calcolarle nei prossimi post)

Ma cosa significa 2x?

2x è tasso di variazione istantaneo della funzione x²

Ciò significa che quando la funzione 2x è positiva (x>0), la funzione principale ha una crescita positiva (f(x) > f(x+k), k∈R)

Aspetta, puoi spiegarmi meglio?

Certo,

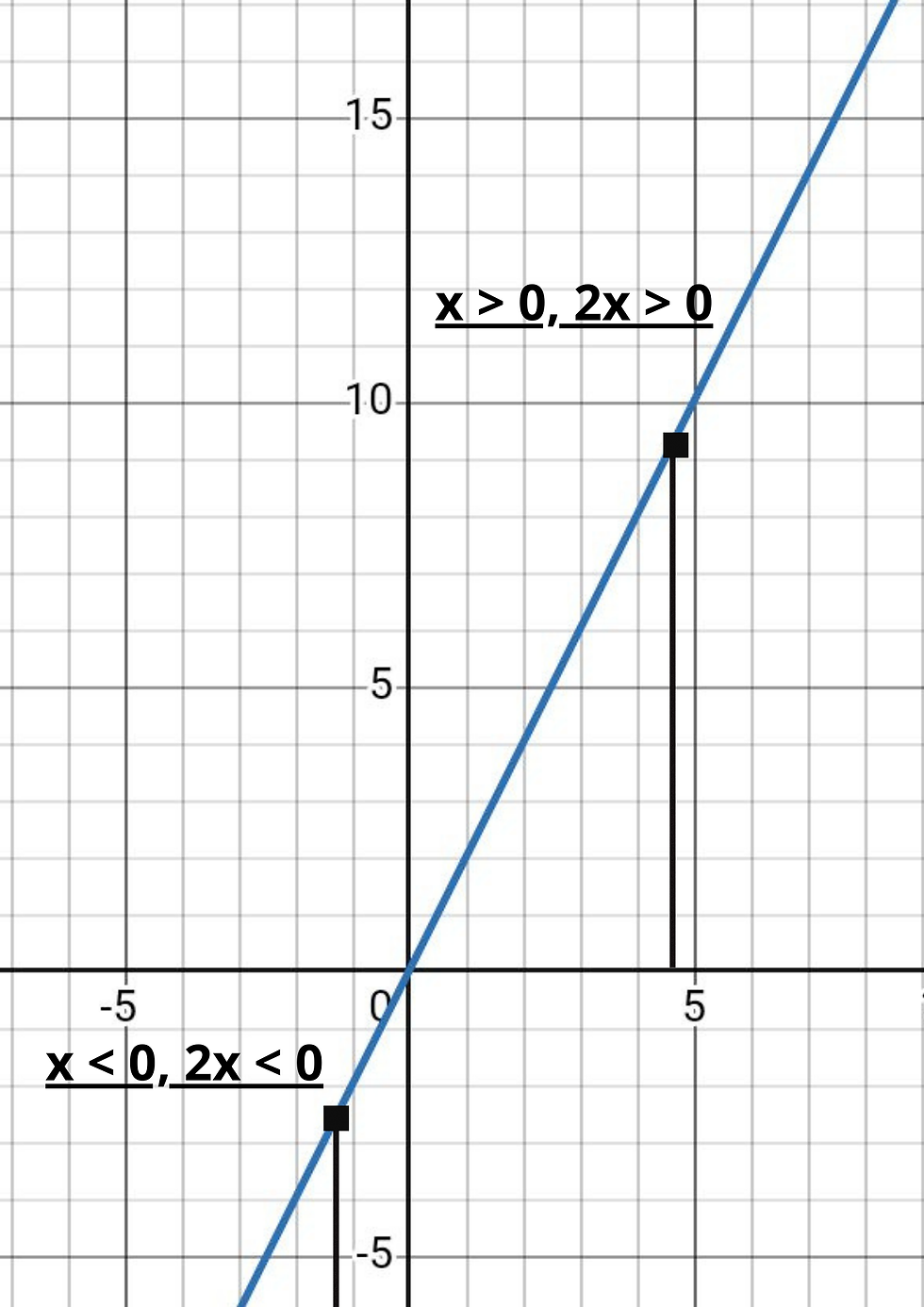
Ecco qua i grafici rispettivamente di x² e 2x:

Notiamo una cosa:

Per valori negativi di x, la derivata (2x) risulta negativa

Dunque allo stesso valore ascissa del grafico della funzione principale, essa è in rapida decrescita

Per valori positivi di x invece, la derivata (2x) risulta positiva, e quindi la funzione principale si mostra in rapida crescita a quel punto

Inoltre…

Un'altra peculiarità della derivata è che il suo valore ad un punto generico x risulta essere la ripidità di una retta tangente alla funzione al punto (x,f(x))

Ciò significa che, in questo caso, con x = 3:

f’(x) = 2x = 2 • 3 = 6

La funzione principale al punto x = 3 risulta 3² = 9

Dunque, sapendo:

x = 3

y = 9

m = 6

[Per una retta generica y = mx + q]

Impostando l'equazione:

9 = 6 • 3 + q

q = -9

Possiamo trovare anche l'intercetta q

Ok, ma a cosa serve questo? Basta che guardo il grafico principale e ragiono…

Beh, sì

Ma ti do altre 2 motivazioni per ricrederti:

1. Una derivata è una funzione a sé che mostra CHIARAMENTE il tasso di crescita della funzione principale senza dover ragionare punto per punto. Questo diventerebbe molto più difficile con funzioni più complesse, rendendo la derivata utile in casi dove abbiamo bisogno di valori precisi non approssimati

2. Come vedremo tra poco, la derivata ci aiuta a trovare i punti di stazionamento con massima precisione, affidandosi alla matematica che è sicuramente più precisa del nostro occhio umano

Aspetta, cos'è questo punto di stazionamento?

Fatta semplice, i punti di stazionamento sono i punti in cui la funzione cambia verso

Da crescente a decrescente, o viceversa

Prendiamo di nuovo la nostra funzione:

Il punto “di svolta”, se così possiamo chiamarlo, possiamo vedere che si trova a (0,0)

A noi ci interessa solo il valore x

Ma come ci aiuta la derivata per questo?

Logicamente, quando avviene un cambio di verso, il tasso di variazione passa da positivo a negativo (o da negativo a positivo)

Passando da un segno all'altro, deve esistere un punto dove la derivata equivale a 0 (si considerano solo funzioni continue)

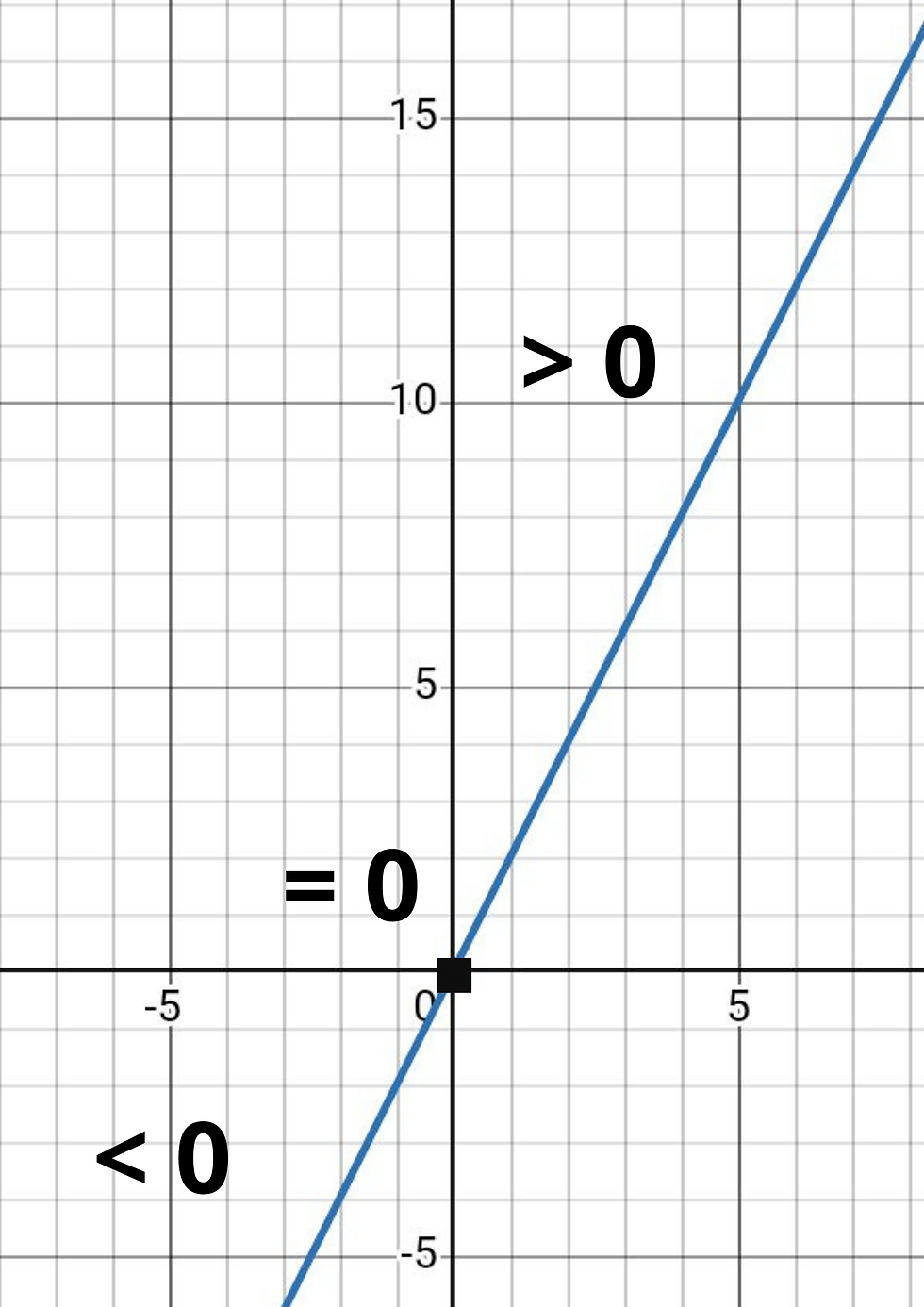
Ed indovinate un po?

Quel punto risulta essere proprio il punto di svolta, in cui la derivata equivale a 0 (dato che non c'è variazione istantanea)

E risolvendo quindi:

f'(x) = 0

2x = 0

x = 0

Questo ci dice che al punto x = 0 la nostra funzione principale risulta stazionaria

Per calcolare la y basterà inserire 0 nella funzione originale

f(x) = x²

f(0) = 0² = 0

Quindi il punto preciso è (0,0) come precedentemente stimato

Ok, credo di aver capito, credo, ma a cosa serve?

Lo scopriremo in un prossimo momento!

- - - - - - - - -

È tutto chiaro? No?

Lo so, è qualcosa di complicato, che non si capisce in 5 minuti di lettura

Tuttavia questo serve solo a gettare delle basi minime per i prossimi post, che potrebbero integrare questi strumenti nei ragionamenti

Non provo sicuramente a spiegarvi dei concetti così avanzati

Ma serve solo per sapere a cosa ci riferiamo quando parliamo di derivate

Detto questo, vi saluto e…

Al prossimo post