Frattali pt. 1

Questo è un frattale...

Bello? Brutto?

Son gusti, ma credo che non cambi il fatto che sia uno dei concetti più strani della matematica complessa...

- - - - - - - - -

Quindi, cos'è un frattale?

Per definizione, un frattale è una figura con INFINITO dettaglio

Ciò significa che, se calcolato con massima precisione, potremmo ingrandire l'immagine e comunque non arrivare ad un limite

Ok, ma cosa significa questo? È comunque un semplice disegno

Beh, no...

Perché, se vi dicessi che questo "semplice disegno" non è in 2D?

Prima però, bisogna introdurre un concetto: la dimensione frattale

Per esprimerla facciamo alcuni esempi:

Sia L una linea 1D, ovvero in una dimensione ( --------- )

Se prendiamo una segmento di lunghezza L / 2, avremmo bisogno di due segmenti di questo tipo per ricomporre L

Quindi diciamo che la sua massa è 1 / 2 (perché ogni segmento L / 2 comporrebbe la metà di L)

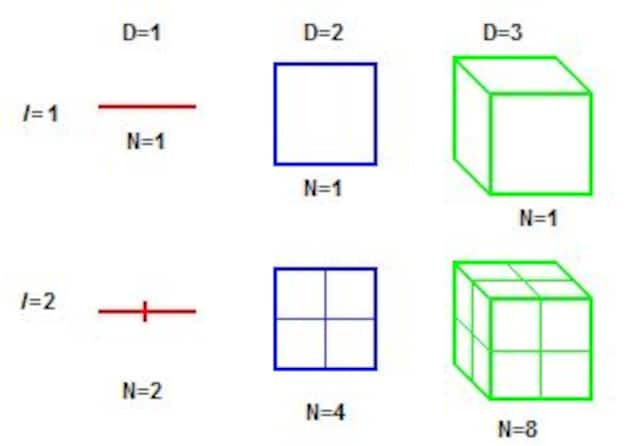
Questo disegno, seppur non di alta qualità, rappresenta bene il concetto

Passando in due dimensioni invece, prendendo un quadrato di lato L ed un altro di lato L / 2:

Il secondo starà 4 volte nel primo come nel disegno. Quindi la sua massa sarà 1 / 4, o 1 / 2²

In 3 dimensioni, un cubo con lato la metà dell'altro starà otto volte nel più grande, quindi avrà massa 1 / 8, o 1 / 2³

Quindi, ricapitolando:

1D | Scala 1:2 | Massa 1 / 2¹

2D | Scala 1:2 | Massa 1 / 2²

3D | Scala 1:2 | Massa 1 / 2³

...lo vedete?

La massa di una figura è esattamente 1 / 2ⁿ, dove n è la dimensione in cui si trova la figura

Ma sappiamo anche che la massa è, la frazione di area occupata dalla figura in scala, rapportata all'area della figura principale

Quindi, per la figura di prima

Vediamo che il triangolo evidenziato è in scala 1:2 rispetto a quello più grande

E ha una massa di 1 / 3, essendo che ne servono 3 per ricomporre la figura principale

Dunque, sapendo questo, possiamo dire che

1 / 3 = 1 / 2ⁿ

La massa è equivalente alla massa espressa in funzione della dimensionalità

Quindi, risolviamo:

Calcolo i reciproci:

3 = 2ⁿ

2ⁿ = 3

Ed estraiamo il logaritmo:

n = log₂(3)

n ≈ 1.585

Aspetta, cosa significa questo? Che la figura ha 1.585 dimensioni?

Sì, ma non per come lo intendiamo noi

Questa è una dimensione frattale

Ma allora perché non è un numero intero? E cosa significa concretamente 1.585 dimensioni?

Semplicemente, la dimensione frattale ci restituisce la complessità di una figura in termini quantitativi

La figura è comunque sul piano 2D, ma il numero 1.585 ci dà un feedback su quanto complessa una figura frattale è

Una figura è più complessa di un'altra quando mostra un perimetro, interno o esterno, meno lineare e meno definito, come le coste di un'isola

Quindi, prendendo una figura "meno complessa" come il fiocco di neve di Koch:

Possiamo vedere come questa figura abbia un perimetro sì frastagliato, ma molto più prevedibile e omogeneo rispetto alla figura iniziale

Inoltre, la sua dimensione frattale riflette questa riflessione, essendo circa 1.26D

Ma alla fine, a cosa servono i frattali nella matematica?

Nella matematica i frattali hanno molti usi e sono molto utili per rappresentare la natura con forme conosciute:

E questo è un esempio di come troviamo le figure frattali dappertutto nella nostra vita, dalla natura agli algoritmi di compressione immagini JPEG come quella che state vedendo...

- - - - - - - - -

Bene...

Questa era solo un'introduzione al mondo dei frattali e pianifico di parlarne ancora in futuro, dato che mi aspetto alcuni dubbi da parte vostra

Il prossimo argomento sarà qualcosa di diverso, e in qualche senso anche complesso, ma non vi preoccupate, renderò tutto più comprensibile...

O almeno ci proverò...

Al prossimo post