Mappa logistica ed equlibrio

Beh...

Non ce l'ho fatta...

Come vedete non riesco a concentrarmi su un argomento solo alla volta...

Ma è questo il bello no?

- - - - - - - - -

Ieri guardando un video sulla mappa logistica mi sono sorpreso della sua complessità, e come numeri tanto simili nella mappa possano portare a risultati completamente diversi

Ma prima di tutto, cos'è una mappa logistica?

Per farla semplice, una mappa logistica ha lo scopo di simulare l'andamento di una popolazione in un determinato habitat, dati due coefficenti: r ed n

• r: rappresenta il tasso di crescita della popolazione, che si calcola come: ( popolazioneₙ - popolazioneₙ₋₁ ) / popolazioneₙ₋₁ dove n è un istante generico

  
  

• n: rappresenta, in percentuale, la popolazione presente in quel ciclo (che può essere annuale, mensile o di qualsiasi durata) in rapporto alla popolazione massima consentita dall'habitat Per esempio, se abbiamo una capacità massima di 100 conigli e ne abbiamo attualmente 20, il nostro valore n sarà: 20 / 100 = 0.2

La mappa si presenta quindi così:

r · n · ( 1 - n )

Ma, per quello che si vede, sembra una semplice parabola di secondo grado, espandendo a:

rn - rn²

E dove sarebbe il fattore ciclo?

Qua viene il trucco...

Non ho mai detto che y = r · n · ( 1 - n )

Bensì:

nₙ = r · nₙ₋₁ · ( 1 - n ₙ₋₁)

Ma cosa significa questo allora?

Semplice... Circa

Per calcolare la popolazione nel prossimo ciclo (n) con nₙ₋₁ che rappresenta la popolazione attuale, troveremo ciò che ci serve sostituendo nella formula i valori r e nₙ₋₁

Ho addirittura creato un programma che simula questa mappa su Python, usando dei grafici complessi e calcoli precisi al millesimo, lo trovate qua: tinyurl.com/2s25nsr3

Questo è un esempio di simulazione dati, con n sull'asse Y ed il ciclo corrente sull'asse X:

r = 2.5 ***

n = 0.5

Vediamo dunque che la popolazione, dopo un momento di oscillazione, trova un punto di equlibrio a n = 0.6

Proviamo con altri numeri ora

D'altronde, questo è il bello delle funzioni:

r = 3.5

n = 0.5

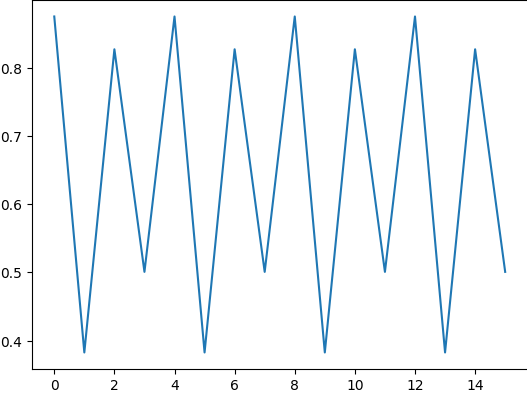
Oh, interessante...

Ora non c'è più un equilibrio...

Tuttavia possiamo comunque identificare una certa regolarità

Per esempio, che per i cicli dispari i valori scendono, e si alternano tra 0.4 e 0.5

Quindi, non esiste un punto di equilibrio, ma comunque abbiamo una certa regolarità...

Ora proviamo con altri dati:

r = 3.8

n = 0.5

Beh, neanche qua abbiamo un equilibrio...

Ma neanche una regolarità...

Quindi?

Andiamo avanti!

r = 4.5

n = 0.5

Ok...

Se i grafici prima avevano almeno un senso logico...

Questo non ha nemmeno senso...

Dato che risultano valori di n < 0

E una percentuale decimale è sempre compresa tra 0 e 1

Ok, abbiamo testato un po' di dati, e abbiamo visto come, cambiando i valori di r, il grafico assume una forma diversa ogni volta

Ma quindi c'è un motivo per questo?

Beh, il motivo è semplice:

Se ripetuto infinite volte, questa mappa restituisce valori diversi in base alla r

Questo è l'unica motivazione...

Strano vero?

Più precisamente:

• Per n ≤ 0: La mappa non ha senso biologico

• Per 0 < n ≤ 1: La mappa ha senso biologico e la specie cala di popolazione ogni ciclo

• Per 1 < n ≤ 3: La mappa ha un tasso di crescita e raggiunge un punto di equilibrio

• Per 3 < n ≤ 3.57: La mappa non raggiunge un punto di equilibrio, ma ha comunque una certa regolarità

• Per 3.57 < n < 4: La mappa non raggiunge un punto di equilibrio e non ha nessuna regolarità

• Per n > 4: La mappa restituisce valori al di fuori dei limiti, non ha senso

Bene, ma ora che sappiamo questo, esiste un modo per calcolare questo punto di equilibrio, quando esiste, senza dover dipendere da questo programma? Certo! Ragionando, il punto di equilibrio si ottiene quando la popolazione del periodo successivo equivale a quella attuale, quindi vale:

r · n · ( 1 - n ) = n

E quindi, procedendo con i calcoli:

r · n · ( 1 - n ) = n

r · ( 1 - n ) = 1

1 - n = ( 1 / r )

-n = (1 / r) - 1

n = 1 - (1 / r)

Quindi, per esempio, con un valore r di 2.5:

n = 1 - (1 / 2.5)

n = 1 - 0.4

n = 0.6

Esattamente quello che abbiamo trovate nel primo caso! ***

Ma dato che io mi complico sempre la vita....

L'ho fatto in un altro modo, più complicato!

Ho dedotto questo:

n₀ = n

n₁ = r n ( 1 - n )

n₂ = r ( r n ( 1 - n ) )( 1 - ( r n ( 1 - n ) )

Dove il pedice sta a significare il ciclo

Come vedete le cose diventano caotiche subito..

Ma se prestiamo attenzione, possiamo notare che le parti sottolineate si equilvalgono

Vedete?

E quindi, per principio di equivalenza:

n₁ = r n ( 1 - n )

n₂ = r ( n₁ )( 1 - ( n₁ )

E questo varrà per tutte le n di questo genere:

nₙ = r · nₙ₋₁ · ( 1 - nₙ₋₁ )

Ed ora, un passaggio fondamentale...

Quando esiste, il punto di equilibrio viene trovato dopo infiniti cicli

Quindi n∞

E dato che n∞-1 , matematicamente parlando, è equivalente a n∞ (Con la regola ∞ ± a = ∞)

Possiamo riscrivere l'equazione come:

n∞ = r · n∞ · ( 1 - n∞ )

Sostituendo n∞ con n:

n = r · n · ( 1 - n )

Ovvero l'equazione precedentemente risolta, con risultato n = 1 - ( 1 / r )

Quindi alla fine, più lavoro, stesso risultato

Credo sia una cosa mia quello di complicarmi la vita...

- - - - - - - - -

Quest'ultima era una mia riflessione sulla mappa logistica e il suo punto di equilibrio, e probabilmente ne ritorneremo a parlare nei prossimi giorni, ma non faccio promesse!

Come sempre, se trovate errori o passaggi non chiari, correggetemi pure nei commenti e ne sarò sempre grato

Un abbraccio e...

Al prossimo post

Per approfondire: www.youtube.com/watch?v=ovJcsL7vyrk