Regressione Lineare: cos'è e come calcolarla

Buon 2025 gente! 🥳🥳🥳

Oggi andremo a vedere una cosa particolare, che però servirà poi ad introdurre concetti più complicati 

Pronti?

- - - - - - - - -

Quando abbiamo un set di dati (punti di coordinate), è utile mostrarli in un grafico per avere un'immagine di ciò che sta succedendo

Ma non sempre porta ai risultati sperati...

Prendiamo un grafico esempio, che correla lo stipendio (€) con la qualità di vita (un indice che va da 1 a 10)

(Grafico fittizio, non c'è nessuna discriminazione verso chi è meno fortunato)

Cosa capiamo da qua?

Possiamo capire, interpretando il trend, che un maggiore stipendio porta ad una migliore qualità di vita (GENERALMENTE)

Ok, ma come possiamo esprimere questa osservazione in termini matematici?

Andando ad approssimare questi dati con una funzione a noi nota:

y = mx + q

Ok, e come trovo i due coefficienti m e q?

Buona domanda, per niente banale, essendo che non possiamo trovarli tanto semplicemente

Quindi, come si fa?

Esistono delle formule, ma non sono tanto fan di usarle alla cieca, quindi ve le spiegherò:

Partiamo da quella per il coefficente angolare:

Il numeratore è la sommatoria del prodotto della differenza (X - X media) e (Y - Y media)

(Y - Y media) è la "distanza" tra il valore Y effettivo e la Y media

Stessa cosa per la X

Poi si fa il prodotto tra le due "distanze"

E si fa la somma per tutti i punti sul grafico

In denominatore abbiamo invece una cosa simile:

La stessa "distanza X" di prima, ma questa volta elevata al quadrato e poi sommata

Per i più scaltri, questa sarà la varianza di X moltiplicata per n (quanti dati abbiamo)

Var(X) • n

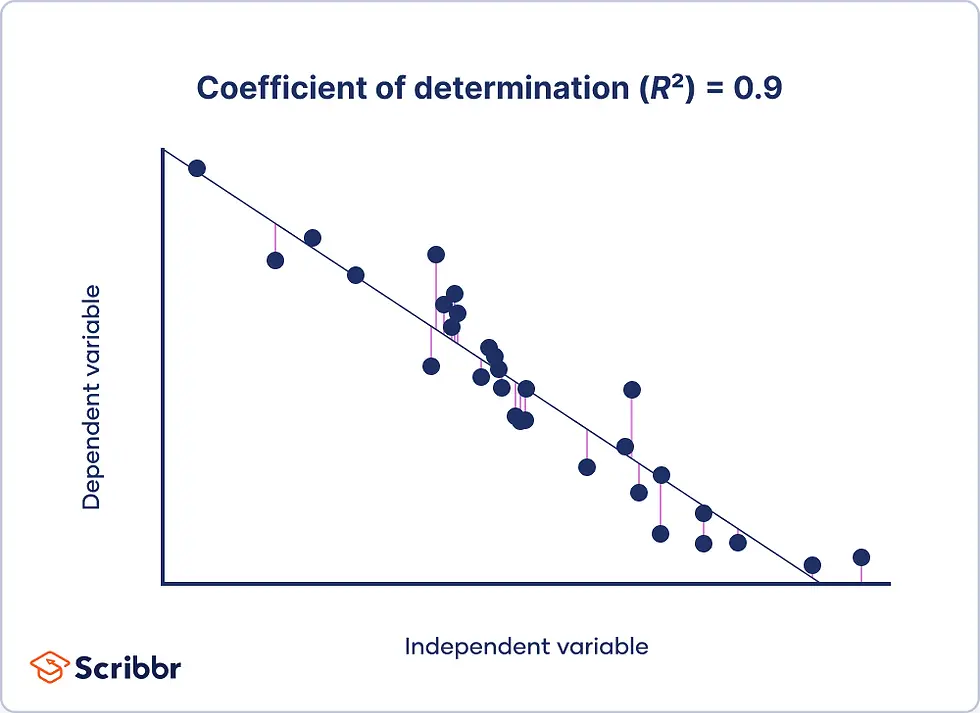
Bene, ma come come posso capire se il modello è una buona approssimazione?

Qua entra in gioco il fattore R² R² = 1 - ( MSE / var(y) )

MSE è il mean squared error:

La "distanza" tra Y e la Y predetta dal modello, al quadrato, per tutti i punti, diviso per il numero di punti

var(y) è la varianza di Y (un modo per calcolare quanto "lontani" sono i dati tra di loro)

Questo fattore varia da 0 a 1, indicando quanto il modello rappresenta fedelmente la realtà

- - - - - - - - -

Ok, nuovo argomento dal nulla, ma servirà per futuri post!

Io vi auguro nuovamente un buon anno a tutti voi e...

Al prossimo post