Derivare e come vengono usate nella vita comune pt. 2

Cos'è questa cosa?

È una derivata, semplicemente visualizzata come una retta tangente alla funzione principale!

L'altra volta abbiamo visto che cos'è una derivata e cosa significa

Ma oggi andremo a vedere i casi in cui possiamo effettivamente applicare questo concetto, oltre a creare queste animazioni

- - - - - - - - -

Piccolo ripasso su che cos'è una derivata di funzione:

Una derivata è una funzione, denominata generalmente con f'(x), che ha come scopo quello di mostrare l'andamento del tasso di crescita istantaneo di una funzione f(x)

Ciò ci aiuta a capire i punti in cui la funzione cresce e quando invece decresce, dandoci anche un "intensità" del fenomeno

Quindi, vediamo alcuni casi in cui le derivate ci possono aiutare

Massimizzazione

Immaginiamo di avere 60m di recinto, e dobbiamo creare un'area per il nostro orticello a casa

Come possiamo usare questi dati per massimizzare l'area pur sapendo che abbiamo solo 60m di perimetro?

Prima di tutto, vogliamo una forma rettangolare, in modo che possiamo calcolare l'area facilmente:

A = b · h    (base per altezza)

E sappiamo anche che b + h + b + h = 60m    (due basi più due altezze)

Dunque:

b + h + b + h = 60m

2b + 2h = 60m

b + h = 30m

b = 30 - h

Sostituendo nell'equazione dell'area:

A = b · h

A = ( 30 - h ) h

Abbiamo espresso l'area con una sola variabile

E se la rendiamo una funzione:

A(h) = ( 30 - h ) h

L'area partendo dall'altezza è ( 30 - h ) h

Se visualizziamo la funzione su un grafico, otteniamo questo:

Una parabola rivolta verso il basso che presenta un punto di picco, dove quindi l'area è massima

(consideriamo solo valori 0 < h < 30, dato che non esistono lunghezze negative nella realtà)

Quindi, come troviamo il punto massimo? Calcoliamo la derivata della funzione A(h) con rispetto a h (la variabile indipendente)

A(h) = ( 30 - h ) h

A(h) = 30h - h²

A'(h) = 30 - 2h

E come sappiamo, il punto di picco di una funzione si trova quando la sua derivata è 0 (quando la funzione passa da crescere a decrescere, o viceversa)

0 = 30 - 2h

2h = 30

h = 15

E ora che abbiamo h, la possiamo sostituire in queste due equazioni di prima:

{ b = 30 - h

{ A = ( 30 - h ) h

{ b = 30 - 15

{ A = ( 30 - 15 ) 15

{ b = 15

{ A = 225

Dunque, il recinto rettangolare di perimetro 60m con area maggiore è quello con:

Altezza 15m

Base 15m

Area 225m²

Trend e andamenti

Immaginiamo di avere questo grafico che mostra l'andamento APPROSSIMATO della disoccupazione in Europa:

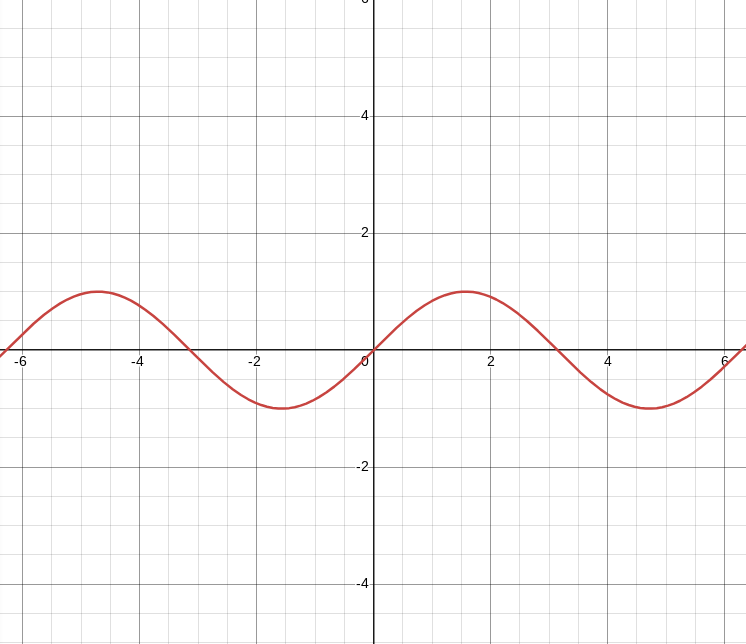
D(t) = sin ( t )

La disoccupazione in funzione del tempo è rappresentata dalla funzione seno

Per capire in un determinato punto storico l'andamento della disoccupazione nel vicino futuro, possiamo usare la derivata:

D(t) = sin ( t )

D'(t) = cos ( t )

E ora, per capire l'andamento della disoccupazione in un determinato periodo, possiamo sostituire l'anno attuale nella funzione

Nell'anno 1:

D(t) = sin ( 1 ) = 0.8415

La disoccupazione è 0.8415 in questo momento

D'(t) = cos ( 1 ) = 0.5402

La disoccupazione è in crescita in questo momento, poichè la derivata è positiva

Dunque, da questa analisi, possiamo dedurre che, nel vicino futuro, la disoccupazione crescerà

Per trovare i punti massimi e minimi invece, dobbiamo impostare la derivata a 0:

D'(t) = cos ( t )

cos ( t ) = 0

t = arccos ( 0 )

t = ( π / 2 ) + 2kπ | k ∈ Z ( Ovvero ( π / 2 ) , ( 3π / 2 ), ( 5π / 2 ) ...)

Dunque, partendo da una funzione di partenza, siamo riusciti a scoprire l'andamento futuro con massima precisione!

(nb. niente è certo nel futuro, e con questo voglio solo dire che lo strumento delle derivate è fatto in modo da essere 100% accurato matematicamente. Le approssimazioni nelle funzioni sono soggette a errore)

(Questo era un esempio puramente numerico, e sono state usate funzioni elementari per semplificare la visualizzazione. Dati del genere non potranno mai essere espressi tanto facilmente)

Analisi sportive

Esatto, la matematica risiede anche negli sport

Prendiamo uno sport che tutti conosciamo, chi più chi meno: La Formula 1

Qua i piloti sono al limite delle proprie capacità, spinte agli estremi dove un minimo errore di progettazione può causare gravi conseguenze

Prendiamo il grafico di una funzione che mostra la velocità della vettura nel tempo (MOLTO approssimativa):

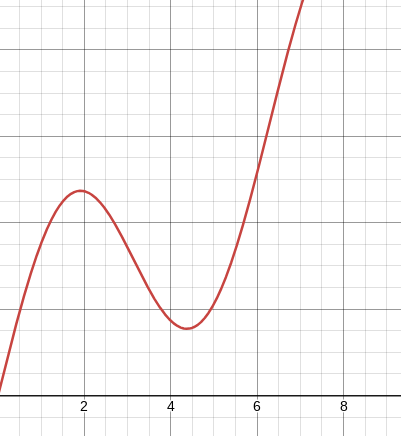
V(t) = 3 sin ( t ) + t

Ora, una peculiarità:

Quando noi calcoliamo la derivata, troviamo il cambiamento istantaneo della funzione in un determinato punto:

Δspazio / Δtempo ( quanto una funzione ( y ) cambia nel tempo ( x ) )

E come sappiamo, spazio / tempo = velocità

Dunque la derivata trova la velocità di cambiamento di una funzione

Se avessimo avuto la funzione spazio della vettura, la sua derivata S'(t) sarebbe stata la velocità in quel momento

Figo?

E allora, la derivata della velocità, che cos'è?

L'accelerazione, definita come ( Δvelocità / Δtempo )

E quindi:

V(t) = 3 sin ( t ) + t

V'(t) = 3 cos ( t ) + 1 Vi risparmio i passaggi

Dunque, possiamo trovare:

• I punti di inizio frenata ( quando la funzione scende sotto lo 0 )

  
  

• I punti di inizio accelerata ( quando la derivata supera lo 0 )

E i corrispettivi periodi di tempo, rendendo l'analisi dei dati più facile e veloce, seppur approssimata in parte

- - - - - - - - -

Ok, oggi abbiamo visto alcune cose, banali per alcuni e affascinanti per altri

Come sempre, spero di avervi passato qualcosa

Se ci sono dubbi non esitate a chiedere qua sotto, io vi auguro un buon proseguimento e...

Al prossimo post